Data smoothing is a very common pre-processing operation on spectral data. Smoothing refer to the numerical operations performed on raw data in order to reduce the (random) noise. This is especially important when we aim at isolating important spectral features that may be partially obscured by the presence of noise.
In some cases, for instance NIR spectroscopy, derivatives of the original scan data are analysed. Numerical differentiation of data amplifies noise enormously and smoothing is mandatory to be able to produce meaningful spectral derivatives.
One of the staple of data smoothing is the Savitzky–Golay (SG) method. The SG method is incorporated in all conventional software packages dealing with chemometrics or multivariate analysis. Most practitioners however, hardly spare any thoughts about the inner workings – and limitations – of the method. Smoothing is reduced, in most cases, to a fixed recipe. This may not be the best scenario in a number of applications, and it may be useful to understand our way around data smoothing, to make sure we can tailor to our application.
In this tutorial we are going to spend some time describing the SG method in Python, the meaning of the parameters, and the limitations of the method. In a future post we will present alternative smoothing methods.
To get up to scratch with some of our other posts on spectral data pre-processing, take a look at the following links
- Two scatter correction techniques for NIR spectroscopy
- NIR data correlograms with Seaborn
- Outliers detection with the Mahalanobis distance and PCA
The data used in this tutorial are taken from the work by J. Cuadros and collaborators: Abundance and composition of kaolinite on Mars: Information from NIR spectra of rocks from acid-alteration environments, Riotinto, SE Spain. The dataset is freely available for download here.
Savitzky–Golay smoothing
The idea behind SG smoothing is quite simple. For each data point in the spectrum, the SG algorithm will:
- Select a window (say, five points) around that point
- Fit a polynomial to the points in the selected window
- Replace the data point in question with the corresponding value of the fitted polynomial.
The parameters to be set by the user are the width of the window and the order of the polynomial to be fitted to the data.
As a quick aside, a special case of polynomial fitting is when we fit a constant value. That is when we replace the central point of the window with the average of all points in that window. This is often called moving average or rolling average.
Ok, back to our problem. Let’s begin our code, as usual, by importing the relevant libraries and loading some of the data:
|
1 2 3 4 5 6 7 8 9 |
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.signal import savgol_filter, general_gaussian data = pd.read_excel('NIR data Earth analogs.xlsx') X = data['C1'].values wl = data['nm'].values |
The data is contained in an Excel spreadsheet. By loading the files without additional options, the first tab of the data file is returned. This will be sufficient for this tutorial, as we are going to use only the very first spectrum (labelled ‘C1’) of the data set.
The basic SG smoothing in Python is done with the savgol_filter function of Scipy:
|
1 2 3 |
w = 5 p = 2 X_smooth_1 = savgol_filter(X, w, polyorder = p, deriv=0) |
In the previous snippet, w is the width of the selection window, while p is the order of the polynomial to be fitted to the data. In the case of a simple smoothing (no derivatives) we set the deriv parameter to 0. To increase the amount of smoothing we have to increase the ratio w/p . For instance, the following parameters will produce a stronger smoothing:
|
1 2 |
X_smooth_2 = savgol_filter(X, 2*w+1, polyorder = p, deriv=0) X_smooth_3 = savgol_filter(X, 4*w+1, polyorder = 3*p, deriv=0) |
Let’s have a check at the results of the previous operation. Let’s plot an interval of the whole spectra, to help the visual assessment
|
1 2 3 4 5 6 7 8 9 10 |
plt.figure(figsize=(9,6)) interval = np.arange(500,600,1) plt.plot(wl[interval], X[interval], 'b', label = 'No smoothing') plt.plot(wl[interval], X_smooth_1[interval], 'r', label = 'Smoothing: w/p = 2.5') plt.plot(wl[interval], X_smooth_2[interval], 'g', label = 'Smoothing: w/p = 5.5') plt.plot(wl[interval], X_smooth_3[interval], 'm', label = 'Smoothing: w/p = 3.5') plt.xlabel("Wavelength (nm)") plt.ylabel("Reflectance") plt.legend() plt.show() |

The blue line is the original spectrum. The red line is a mild smoothing with w/p = 2.5, the green line represents a more aggressive smoothing and the magenta line is a more optimal choice of parameters.
How to choose the parameters of the Savitzky–Golay smoothing function
Let’s explain the rationale behind these choices. The spectrum we are dealing with is in the NIR region, which means it contains features that vary fairly gently with the wavelength. If you go ahead and plot the whole spectrum you’ll see how NIR oscillation are always very smooth as they come from mixing of overtones of the fundamental resonances. This means that, once we have set a window width, the data inside that window can always be approximated well with a fairly low order polynomial.
Note that this might not be the case for sharper peaks (think of MIR or Raman peaks). In this case you are better off increasing the order of the polynomial. Keep in mind however that increasing the order too much (without increasing the window width as well) would produce a polynomial that will start closely following the noise oscillations of the spectrum. This would obviously be a bad choice, as we would like to get rid of those oscillations.
How about the window width? Well, we need to set a width that is small compared to the main features of our spectrum, and large compared to the noise. Looking at the plot above, a width of 5 pixels is comparable with the noise oscillation width, and therefore is not very effective in removing them (see red line). Setting the width to 11 instead, does a much better job in smoothing out the noise. Note that however 11-point smoothing is reducing the contrast of the 1410 nm trough as well. In our case the reduction is fairly mild, however increasing the width even further must be done with caution, as we’d start to wash away the important features of the spectrum.
To get a (slightly) better result we can increase window width and polynomial order at once, in such a way to reach a ratio w/p = 3.5 which is in between the previous two cases. That is represented by the magenta line in the figure above, which smooths out the noise oscillation pretty well, yet it follows the peak trough more closely.
Let’s explain this last choice in more detail. We wish to increase the window width to be more effective against the noise. Over such a larger width a second order polynomial is no longer a good approximation to the data, therefore we need to increase the polynomial order as well.
For a more advanced tutorial on parameters selection, see our newer post here.
Savitzky–Golay smoothing of derivative spectra
As mentioned, in many cases, derivatives of the spectra can be used to increase sensitivity. Numerical differentiation amplifies small variations in the data, thus improving the contrast of relevant spectral features. Just as well however, it amplifies the noise in the data.
Therefore we have basically no way around smoothing. If we want to use derivatives, we’ve got to to smooth the data. The handy savgol_filter function enables this by adding another parameter, i.e. by setting the deriv parameter to a non-zero value.
Under the hood, the function will perform a numerical differentiation, then apply the SG method to the resulting differential spectrum.
For example, let’s look at the second derivative spectrum, using the same set of parameters used before.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
w = 5 p = 2 X2_smooth_1 = savgol_filter(X, w, polyorder = p, deriv=2) X2_smooth_2 = savgol_filter(X, 2*w+1, polyorder = p, deriv=2) X2_smooth_3 = savgol_filter(X, 4*w+1, polyorder = 3*p, deriv=2) plt.figure(figsize=(9,6)) plt.plot(wl[interval], X2_smooth_1[interval], 'r', label = 'Smoothing: w/p = 2.5') plt.plot(wl[interval], X2_smooth_2[interval], 'g', label = 'Smoothing: w/p = 5.5') plt.plot(wl[interval], X2_smooth_3[interval], 'm', label = 'Smoothing: w/p = 3.5') plt.xlabel("Wavelength (nm)") plt.ylabel("Second Derivative Reflectance") plt.legend() plt.show() |
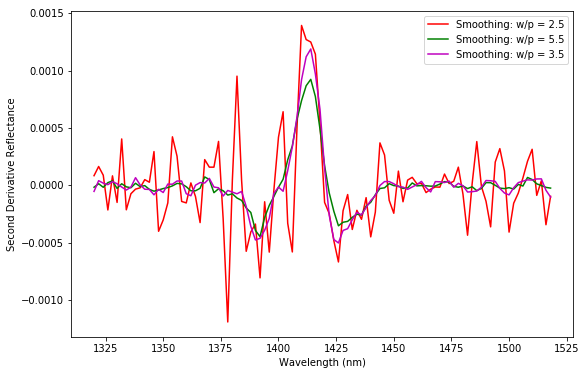
It’s clear that the mild smoothing (in red) is quite ineffective. The red curve is still significantly noisy. The green curve is arguably too smooth instead. You can notice that the contrast of the main features is quite reduced as a result of the large window. Once again the parameters used for the magenta line are better. Some residual noise is still present but the curve captures the main features of the second derivative spectrum without excessively washing out the contrast.
One of the problems of Savitzky–Golay smoothing
One of the common problems of derivative smoothing with SG method is that the first points of the spectra can be lost after smoothing. Let’s look at the previous data, by focusing on the first 100 points of the second derivative spectra.
|
1 2 3 4 5 6 7 8 9 |
init_inter = np.arange(0,100,1) plt.figure(figsize=(9,6)) plt.plot(wl[init_inter], X2_smooth_1[init_inter], 'r', label = 'Smoothing: w/p = 2.5') plt.plot(wl[init_inter], X2_smooth_2[init_inter], 'g', label = 'Smoothing: w/p = 5.5') plt.plot(wl[init_inter], X2_smooth_3[init_inter], 'm', label = 'Smoothing: w/p = 3.5') plt.xlabel("Wavelength (nm)") plt.ylabel("Second Derivative Reflectance") plt.legend() plt.show() |

In the case of red and green curve, the data has become constant over an extent equal to the window width. This is a natural consequence of the choice of parameters we make. We chose to use a second order polynomial, which obviously reduces to a constant upon second derivative. The magenta line however doesn’t suffer from the same problem, as we used a sixth order polynomial which reduces to a fourth order one after double derivation. Whether the edge data is significant or not however is another story.
Here’s the take-home message. If you’ve got a large number of points in the spectrum, you can probably afford to loose a few of them at the edges of your wavelength band. However if you do not have this many spectral point – or your data is quite noisy, thus requiring a larger smoothing window – you may want to be extra careful to try and hold on to these edge points.
Wrap up
In this tutorial we discussed the inner workings on the Savitzky–Golay smoothing method. When analysing a new set of spectral data is important to spend a little time checking the parameters of the smoothing filter are appropriate for our type of data. Do not rely on fixed recipes or copy-paste code: always check the best choice of window width and polynomial order depending on the relevant features of your data.
Hope you enjoyed the post. If you found it useful, please share it with a friend and help us grow. Thanks for reading!



